抱歉，您的浏览器无法访问本站
本页面需要浏览器支持（启用）JavaScript
了解详情 >

数据结构笔记 -- 排序

编程技术

发布于：2024年9月30日

关于排序知识的整理总结

1.0 基本概念

​ 有 n 个记录的序列{R1，R2，…，Rn}，其相应关键字的序列是{K1，K2， …，Kn }，相应的下标序列为1，2，…，n`。

通过排序，要求找出当前下标序列1，2，…， n的一种排列p1，p2， …，pn，使得相应关键字满足如下的非递减（或非递增）关系，即：Kp1≤ Kp2≤…≤ Kpn ，这样就得到一个按关键字有序的记录序列：{Rp1，Rp2， …， Rpn}。

（1）数据表

待排序数组元素的有限集合。

（2）主关键字与次关键字

上面所说的关键字 Ki 可以是记录 i 的主关键字，也可以是次关键字，甚至可以是记录中若干数据项的组合。

若 Ki 是主关键字，则任何一个无序的记录序列经排序后得到的有序序列是唯一的。若 Ki 是次关键字或是记录中若干数据项的组合，得到的排序结果将是不唯一的，因为待排序记录的序列中存在两个或两个以上关键字相等的记录。

（3）内部排序与外部排序

内部排序：整个排序过程不需要访问外存便能完成

外部排序：参加排序的记录数量很大，整个序列的排序过程不可能在内存中完成，需要借助外存

（4）主关键字与次关键字

若两个记录 A 和 B 的关键字值相等，若排序后 A、B 的先后次序保持不变，则称这种排序算法是稳定的，反之称为不稳定的

（5) 逆序

在一个排列中，如果一对数的前后位置与大小顺序相反，即前面的数大于后面的数，那么它们就称为一个逆序。 一个排列中所有逆序的总数叫做这个排列的逆序数。

（6）算法的优劣性

  • 时间效率：排序速度(排序所花费的全部比较次数)

  • 空间效率：占内存辅助空间的大小

  • 稳定性：排序是否稳定

2.0 基本排序方法

2.1 冒泡排序

算法思想：每趟对所有记录从左到右相邻两个记录进行比较，若不符合排序要求，则进行交换。直到所有相邻元素都满足要求,则算法结束。使用前提必需是顺序存储结构。

时间复杂度: (n−1)+(n−2)+…+1+0=n(n−1)/2

  • 最坏情况=O(n^2)

  • 最好情况:O(N)

空间复杂度: ** 由于算法在执行过程中，只有「交换」变量时候采用了临时变量的方式，而其它没有采用任何的额外空间，所以空间复杂度为O( 1 )**。

算法实现:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
//冒泡排序
void BubbleSort(int* arr, int n)
{

        for (int i = 0; i < arr.length - 1; i++) {
            for (int j = 0; j < arr.length - 1 - i; j++) {
                if (arr[j] > arr[j + 1]) {
                    int temp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = temp;
                }
            }
        }
}

代码优化:

(1) 减少检验轮数: 通过设置一个交换标志，如果某次循环没有发生交换操作，则说明序列已经有序：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

      //定义一个标志位，用于判定元素之间是否进行了交换
//Boolean 变量存储为 16 位（2 个字节）的数值形式，但只能是 True 或是 False
      boolean flag = false;

      for (int i = 0; i < arr.length - 1; i++) {
          for (int j = 0; j < arr.length - 1 - i; j++) {
              if (arr[j] > arr[j + 1]) {
                  flag = true;
                  int temp = arr[j];
                  arr[j] = arr[j + 1];
                  arr[j + 1] = temp;
              }
          }
          if (!flag) {
              break;
          } else {
              //如果发生了交换，那么在下一轮排序之前将flag再次置为false,以便记录下一轮排序的时候是否会发生交换
              flag = false;
          }
      }

(2) 鸡尾酒排序: 冒泡排序算法每一轮都是从左到右进行元素比较，进行单向的位置交换，鸡尾酒排序算法则是双向的元素比较和交换。

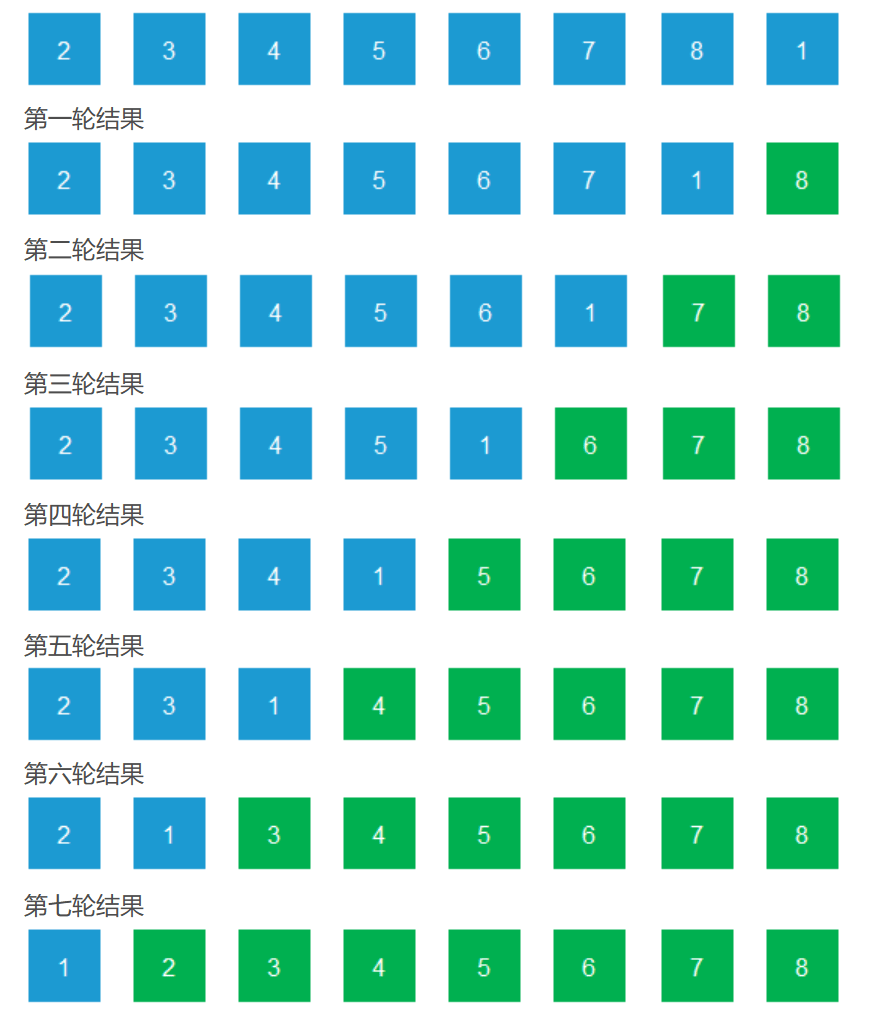
例题: 排序以下序列

冒泡排序思想:

由上面可以看出，从 2 到 8 已经是有序了。只有元素 1 的位置不对，却还要进行 7 轮排序。而鸡尾酒算法可以解决这一问题。

鸡尾酒排序:

第一轮

与冒泡排序一致，从左到右进行比较、交换

image-20241230201902247

第二轮

则从右向左进行比较、交换
image-20241230201905749 > 20200807102110583

第三轮

没有发生任何元素交换，说明序列已是有序的，排序结束。

image-20241230201910465

代码实现:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
void Cocktail_Sort(int arr[], int sz)
{
	int tmp = 0;
	int left = 0;
	int right = sz - 1;
	for (int i = 0; i < sz / 2; i++)
	{
		//有序标记，每一轮的初始是true
		int flag = 1;

		//奇数轮，从左向右比较和交换
		for (int j = 0; j < sz - i - 1; j++)
		{
			if (arr[j] > arr[j + 1])
			{
				tmp = arr[j];
				arr[j] = arr[j + 1];
				arr[j + 1] = tmp;

				//有元素交换，所以不是有序，标记变为0
				flag = 0;
			}
		}

		if (flag)
			break;

		//偶数轮之前，重新标记为1
		flag = 1;

		//偶数轮，从右向左比较和交换
		for (int j = sz - i - 1; j > i; j--)
		{
			if (arr[j] < arr[j - 1])
			{
				tmp = arr[j];
				arr[j] = arr[j - 1];
				arr[j - 1] = tmp;

				//有元素交换，所以不是有序，标记变为0
				flag = 0;
			}
		}

		if (flag)
			break;
	}
}

void Cocktail_Show(int arr[], int sz)
{
	int i = 0;

	for (i = 0; i < sz; i++)
	{
		printf("%d ", arr[i]);
	}
	printf("\n");
}

int main()
{
	int arr[] = { 2,3,4,5,6,7,8,1 };
	int sz = sizeof(arr) / sizeof(int);

	printf("排序前:");
	Cocktail_Show(arr, sz);//打印排序函数

	Cocktail_Sort(arr, sz);//排序函数

	printf("排序后:");
	Cocktail_Show(arr, sz);

	return 0;
}

代码优化:

思路同冒泡排序,但由于鸡尾酒排序是双向的,需要设定两个边界值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
void Cocktail_Sort(int arr[], int sz)
{
	int tmp = 0;

	//无序数列的左边界，每次比较只需要比到这里为止
	int leftBorder = 0;

	//无序数列的右边界，每次比较只需要比到这里为止
	int rightBorder = sz - 1;

	//记录右侧最后一次交换的位置
	int lastRightExchange = 0;

	//记录左侧最后一次交换的位置
	int lastLeftExchange = 0;

	for (int i = 0; i < sz / 2; i++)
	{
		//有序标记，每一轮的初始是true
		int flag = 1;

		//奇数轮，从左向右比较和交换
		for (int j = leftBorder; j < rightBorder; j++)
		{
			if (arr[j] > arr[j + 1])
			{
				tmp = arr[j];
				arr[j] = arr[j + 1];
				arr[j + 1] = tmp;

				//有元素交换，所以不是有序，标记变为0
				flag = 0;
				lastRightExchange = j;
			}
		}

		rightBorder = lastRightExchange;
		if (flag)
			break;

		//偶数轮之前，重新标记为1
		flag = 1;

		//偶数轮，从右向左比较和交换
		for (int j = rightBorder; j > leftBorder; j--)
		{
			if (arr[j] < arr[j - 1])
			{
				tmp = arr[j];
				arr[j] = arr[j - 1];
				arr[j - 1] = tmp;

				//有元素交换，所以不是有序，标记变为0
				flag = 0;
				lastLeftExchange = j;
			}
		}
		leftBorder = lastLeftExchange;
		if (flag)
			break;
	}
}

2.2 插入排序和希尔排序

算法思想: 每步将一个待排序的元素按照其关键字的值,插入到前面已经排序好的一组数组中适当的位置,使其仍然保持有序。

时间复杂度:

  • 最好情况：数组是有序的或者接近有序的，那么时间复杂度为：O(N)
  • 最坏情况：数组是逆序的，那么时间复杂度为：O(N^2)

空间复杂度：O(1)

算法实现:

1) 直接插入
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
void InsertSort(int* a, int n) {
	//数组的长度是n，那么最后一个数据是n-1，倒数第二个数据是n-2
	for (int i = 0; i < n - 1; ++i) {
		// [0 end]有序，把end+1的位置的值插入进去，保持它依旧有序
		int end = i; //记录有序序列的最后一个元素的下标
		int tmp = a[end + 1]; //待插入的元素
		while (end >= 0) {
			if (tmp < a[end]) {
				a[end + 1] = a[end];
				--end;
			}
			else {
				break;
			}
		}
		//代码执行到此位置有两种情况:
		//1.待插入元素找到应插入位置（break跳出循环到此）。
		//2.待插入元素比当前有序序列中的所有元素都小（while循环结束后到此）。
		a[end + 1] = tmp;
	}
}

相关文章
数据结构笔记 -- 队列关于队列知识的总结,附源教学网站ARIES算法基于 undo/redo 日志的恢复算法缺陷、ARIES 优化策略、脏页表作用、活跃事务表和 PrevLSN

更新于：2024年12月30日

数据结构

评论