之前写的 verilog 笔记，记得很混乱，但还是传一下吧

数据类型

基本模块:

1
2
3
4
5
6
7
8
9
10
11
12

module 模块名 (
    // 端口定义之间用英文逗号 , 分隔开
    输入端口定义,         // 输入端口只能是 wire 类型
    输出端口定义          // 输出端口可以根据需要定义为 wire 或 reg 类型
);                      // 不要忘记这里的分号

    内部信号定义语句       // 内部信号可以根据需要定义为 wire 或 reg 类型
        //wire型可省略
    模块实例化语句         // 将其他模块接入电路
    assign 数据流赋值语句
    always 过程赋值语句
endmodule

线网（wire）

wire 类型表示硬件单元之间的物理连线，由其连接的器件输出端连续驱动。如果没有驱动元件连接到 wire 型变量，缺省值一般为 “Z”。举例如下：

实例

1
2
3

wire  interrupt ;
wire  flag1, flag2 ;
wire  gnd = 1'b0 ;

线网型还有其他数据类型，包括 wand，wor，wri，triand，trior，trireg 等。这些数据类型用的频率不是很高，这里不做介绍。

寄存器（reg）

寄存器（reg）用来表示存储单元，它会保持数据原有的值，直到被改写。声明举例如下：

实例

1
2

reg   clk_temp;
reg  flag1, flag2 ;

例如在 always 块中，寄存器可能被综合成边沿触发器，在组合逻辑中可能被综合成 wire 型变量。寄存器不需要驱动源，也不一定需要时钟信号。在仿真时，寄存器的值可在任意时刻通过赋值操作进行改写。例如：

实例

1
2
3
4
5
6

reg rstn ;
initial begin
  rstn = 1'b0 ;
  #100 ;
  rstn = 1'b1 ;
end

wire 和 reg 的区别

1.wire 和 reg 的本质

wire 的本质是一条没有逻辑的连线，也就是说输入时什么输出也就是什么。wire 型数据常用来表示以 assign 关键字指定的组合逻辑信号，模块的输入输出端口类型都默认为 wire 型，wire 相当于物理连线，默认初始值是 z（高组态）。
如果你把 wire 定义的变量用在有逻辑性的语句中就会出现综合错误：
例如：
在 always 语句中使用 wire 型定义的变量赋值，综合器就会报错。

reg 型表示的寄存器类型，用于 always 模块内被赋值的信号，必须定义为 reg 型，代表触发器，常用于时序逻辑电路，reg 相当于存储单元，默认初始值是 x（未知状态）。reg 型相对复杂些，其综合后的输出主要还看具体使用的场景：当在组合电路中使用 reg，合成后的仍然是 net 网络；当在时序电路中使用 reg 合成后的才是 register。

2.wire 和 reg 在硬件描述语言中的释义

关于 wire 和 reg 在硬件描述语言中的释义一般需要分为以下两个部分来分析：
从电路综合角度来说
（1）wire 型变量综合出来是一根导线
（2）reg 型在 always 语句模块中又分为两种情况
(a) always 后的敏感表中是（a or b or c）形式的，也就是不带时钟边沿的，综合出来还是组合逻辑
(b) always 后的敏感表中是（posedge clk）形式的，也就是带边沿的，综合出来一般是时序逻辑，会包含触发器（Flip－Flop）

在设计中，输入信号一般来说你是不知道上一级是寄存器输出还是组合逻辑输出，那么对于本级来说就是一根导线，也就是 wire 型。而输出信号则由你自己来决定是组合逻辑输出还是寄存器输出，wire 型、reg 型都可以。但一般的，整个设计的外部输出（即最顶层模块的输出），要求是寄存器输出，较稳定、扇出能力也较好。

从仿真分析角度来说
wire 对应于连续赋值，如 assign
reg 对应于过程赋值，如 always，initial

3.使用 wire 的情况

（1）assign 语句中变量需要定义成 wire 型
例如：

1
2
3
4

reg a,b;
wire result;
…
assign result =a&&b;

（2）元件例化时候的输出必须用 wire
例如：

1
2
3
4
5
6
7
8

wire dout;

ram u_ram
(
…
.out(dout)
…
);

（3）input、output 和 inout 的预设值都是 wire

input、inout 类型的端口不能声明为 reg 数据类型，因为 reg 类型常用于保存数值，而输入端口只反映与其相连的外部信号的变化，不应保存这些信号的值。output 类型的端口则可以声明为 wire 或 reg 数据类型。

wire 型为默认数据类型，因此当端口为 wire 型时，不用再次声明端口类型为 wire；但是当端口为 reg 型时，对应的 reg 声明不可省略。

整数（integer）

整数类型用关键字 integer 来声明。声明时不用指明位宽，位宽和编译器有关，一般为 32 bit。reg 型变量为无符号数，而 integer 型变量为有符号数。

综合后实际电路里并没有 k这个信号

k只是辅助生成相应的硬件电路。

状态机

**FSM **

FSM 的概念

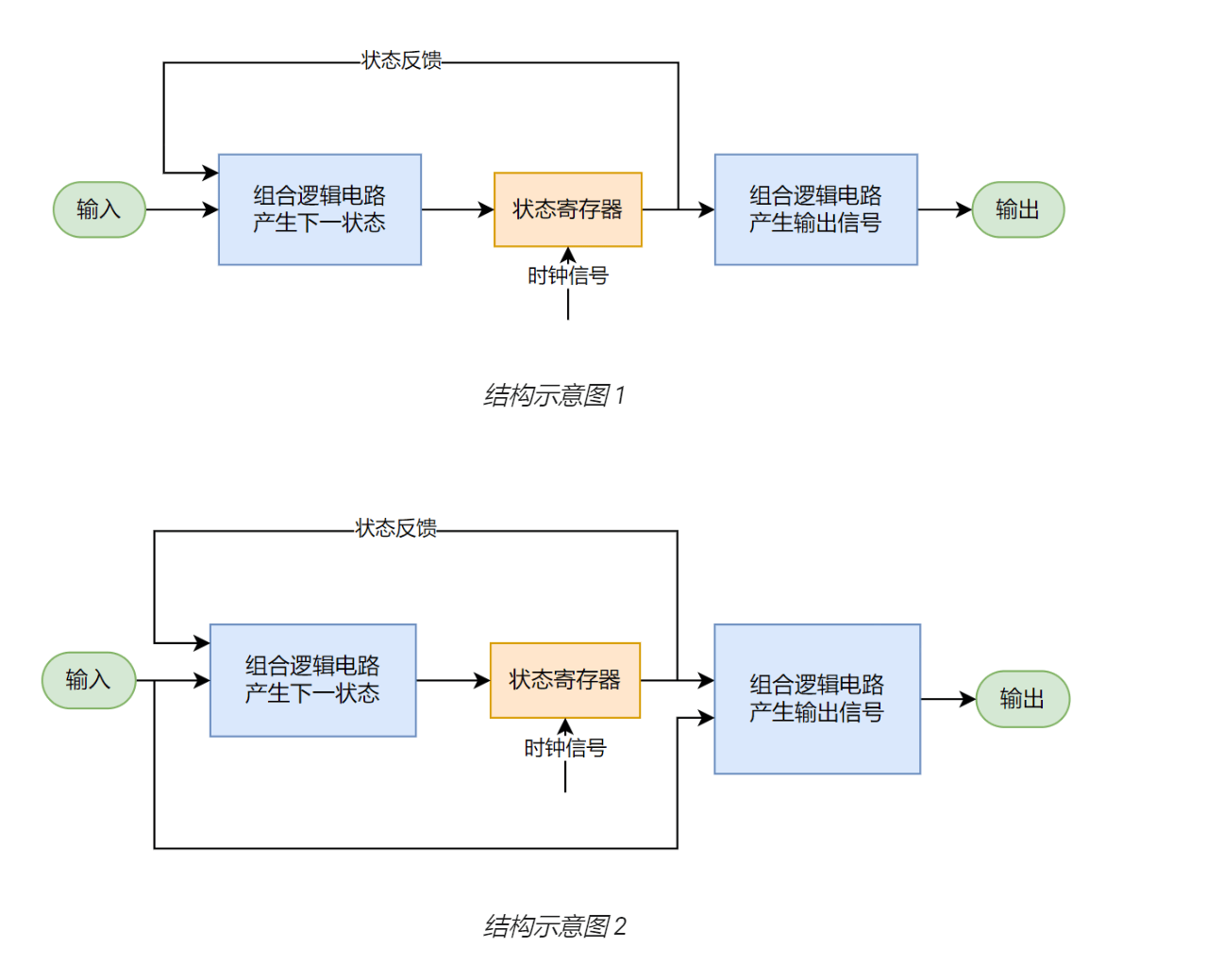
注意到电路中存在一个名为状态寄存器的特殊结构，该结构存储了电路当前的状态信息。设寄存器位宽为 n，则该电路的状态数量不会超过 2 的 n 次方，即其状态数量是有限的，因此这种电路结构称为有限状态机（FSM）。

顾名思义，有限状态机就是由一系列数量有限的状态组成的循环机制。它是由寄存器和组合逻辑构成的硬件时序电路。状态机通过控制各个状态的跳转来控制流程，使得整个代码看上去更加清晰易懂，在控制复杂流程的时候，状态机有着明显的设计优势。

设计 FSM

（1）画出状态转移图

把实际系统进行逻辑抽象，即实际问题转化为设计要求。首先确定电路输入输出引脚；然后根据实际需要列出所有的状态情况，并对状态顺序进行编号；最后根据状态转移条件画出状态转移图。

（2）确定状态编码和编码方式

编码方式的选择对所设计的电路复杂与否起着重要作用，要根据状态数目确定状态编码和编码方式。

（3）给出状态方程和输出方程

列写状态转移表，选定触发器类型，通过卡诺图化简给出状态方程和输出方程。（此步在 FPGA 编程中可省略）

（4）编写 Verilog 代码

按照步骤（1）~（2）编写具有可综合的 Verilog 代码。

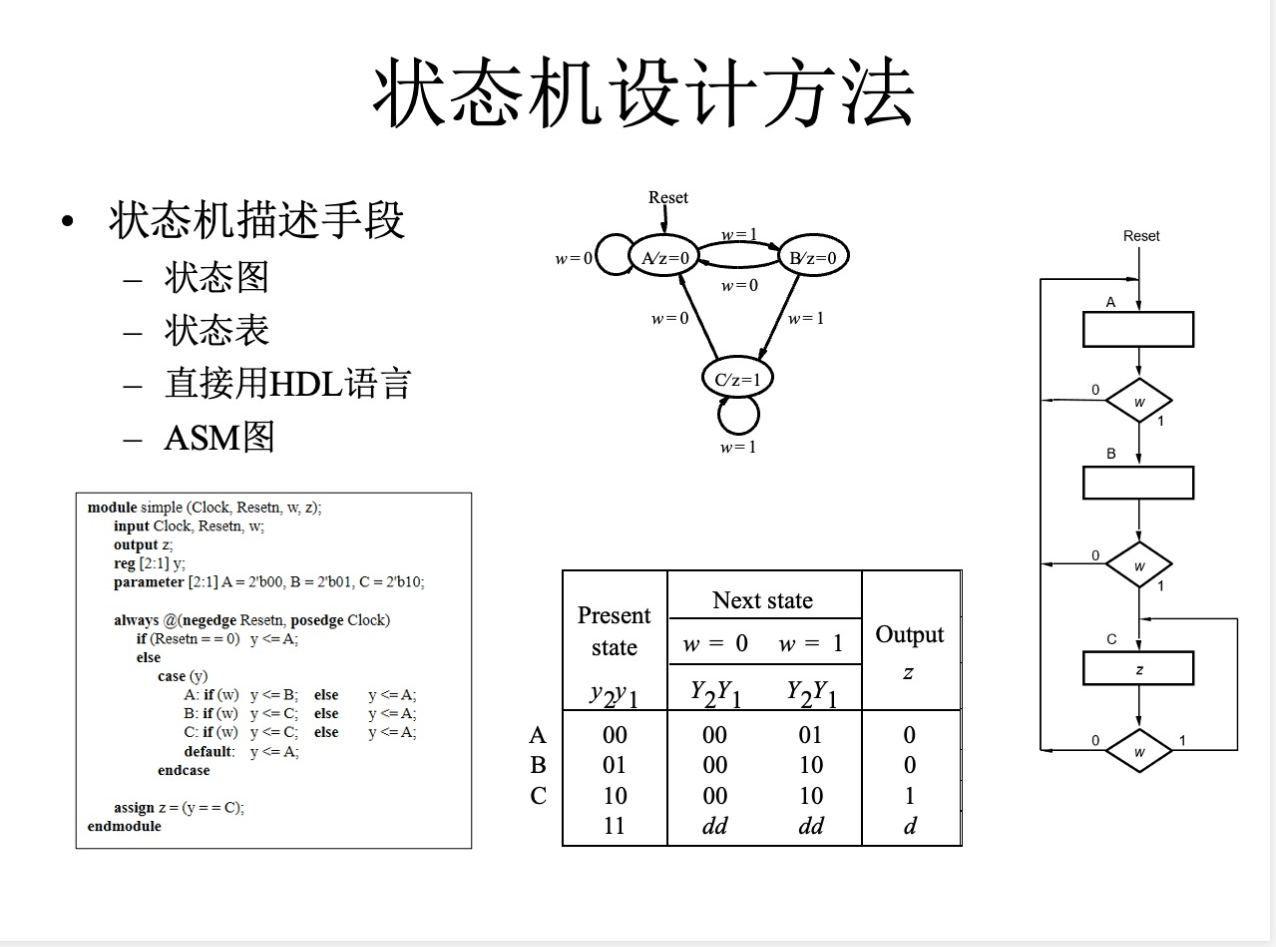
状态机分类：moore 和 mealy

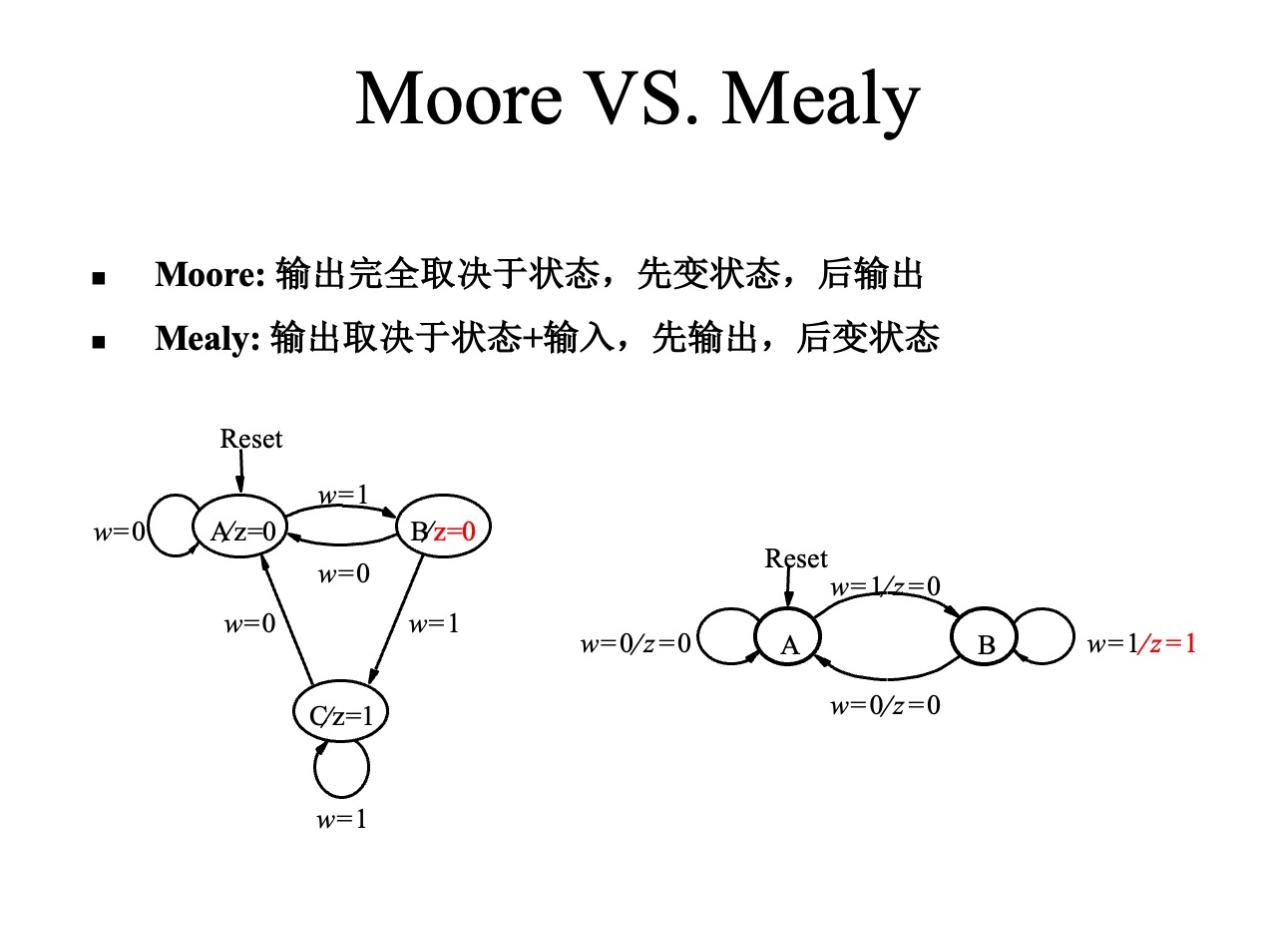
• Moore：输出信号只与现态有关，输入信号不会直接影响到输出信号，而是与当前状态（简称现态）信号一起生成下一状态（简称次态）信号，在时钟的上升沿之后次态转换为现态，才能影响到输出
• Mealy：输出信号由现态与输入信号共同生成，输入信号可立刻对输出信号产生影响

两种结构的有限状态机各有优缺点：Moore 型时序更好，但响应要慢一拍，Mealy 型响应最快，但时序上要差一些。一般来说，如果对电路相应速度要求不是非常苛刻的话，推荐使用 Moore 型有限状态机。

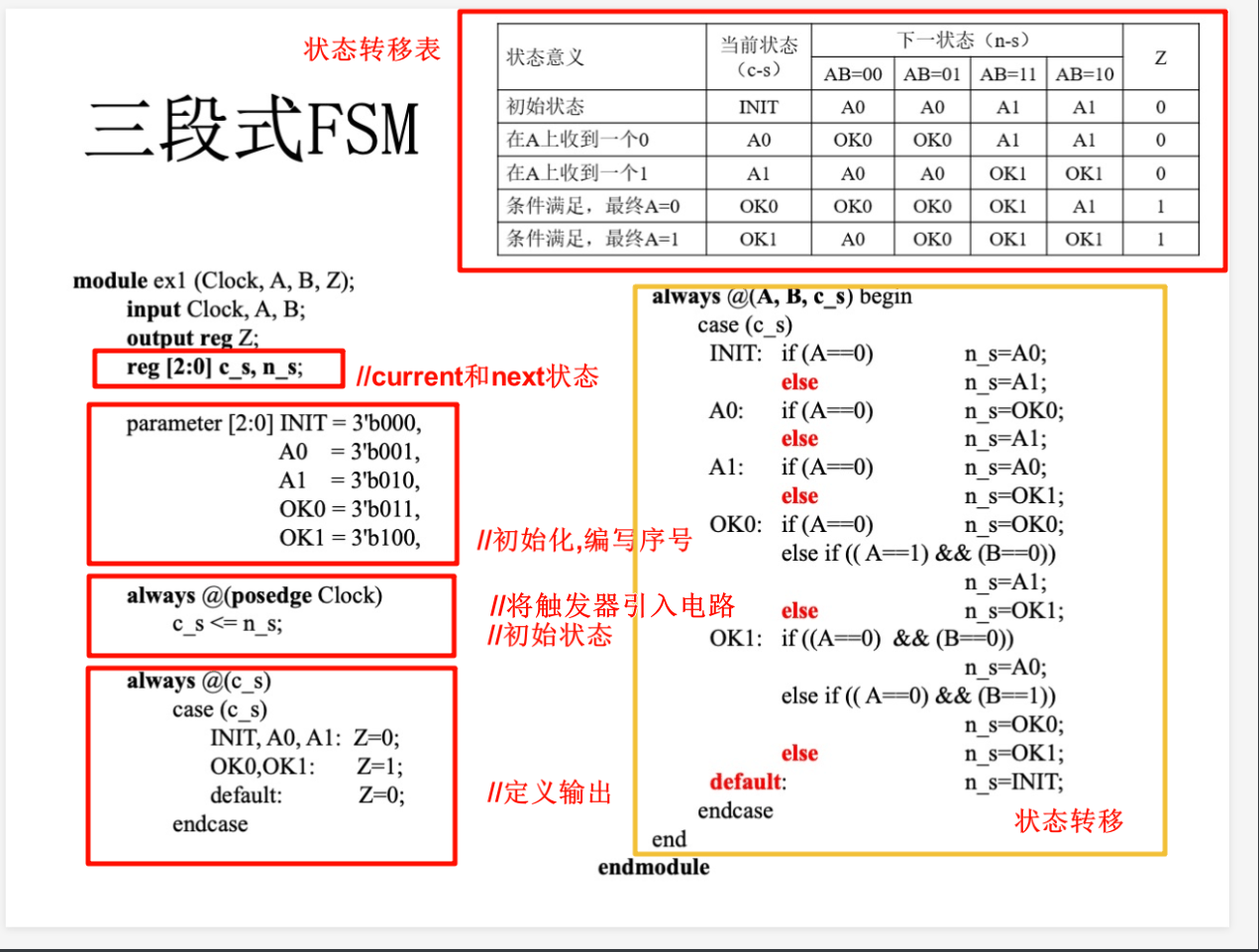
FSM 代码实现

结构

通过分析有限状态机的结构图，我们可以发现其包含三个部分：

• 第一部分为组合逻辑，通过现态和输入信号生成次态信号。
• 第二部分为时序逻辑，包含一个带有复位功能的寄存器单元，复位时现态信号变为初始值，否则在每个时钟的上升沿将次态信号赋值给现态信号。
• 第三部分为组合逻辑，该部分通过现态信号生成各输出信号。

其对应的代码结构为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71

module FSM (
    input           clk,
    input           rst,
    // ......
    // 其他输入输出信号
);
// 状态空间位数 n
parameter WIDTH = 3;

// 状态变量
reg [WIDTH-1: 0] current_state, next_state;
// 为了便于标识，我们用局部参数定义状态的别名代替状态编码
localparam STATE_NAME_1 = 3'd0;
localparam STATE_NAME_2 = 3'd1;
// ......

// ==========================================================
// Part 1: 使用同步时序进行状态更新，即更新 current_state 的内容。
// ==========================================================
always @(posedge clk) begin
    // 首先检测复位信号
    if (rst)
        current_state <= RESET_STATE;
    // 随后再进行内容更新
    else
        current_state <= next_state;
end

// ==========================================================
// Part 2: 使用组合逻辑判断状态跳转逻辑，即根据 current_state 与
//         其他信号确定 next_state。
// ==========================================================
// 一般使用 case + if 语句描述跳转逻辑
always @(*) begin
    // 先对 next_state 进行默认赋值，防止出现遗漏
    next_state = current_state;
    case (current_state)
        STATE_NAME_1: begin
            // ......
        end
        STATE_NAME_2: begin
            // ......
        end
        default: begin
            // ......
        end
    endcase
end

// ==========================================================
// Part 3: 使用组合逻辑描述状态机的输出。这里是 mealy 型状态机
//         与 moore 型状态机区别的地方。
// ==========================================================
// 可以直接使用 assign 进行简单逻辑的赋值
assign out1 = ......;
// 也可以用 case + if 语句进行复杂逻辑的描述
always @(*) begin
    case (current_state)
        STATE_NAME_1: begin
            // ......
        end
        STATE_NAME_2: begin
            // ......
        end
        default: begin
            // ......
        end
    endcase
end
endmodule

一个实例

数字锁

某助教有一个神奇的锁。锁盘上只有两个按键，我们不妨记为 0 和 1。只有按键按照 0100 的顺序按下时才能解锁成功。例如，连续按下 01010 时并不会解锁，但再按下 0 后便会解锁（因为最近的四次输入为 0100）。我们想用一个数字电路判断给定的按键顺序能否解锁。

模块的输入包含一个时钟信号 clk 以及按下的按键编号 in。由于只有两个按键，所以我们可以根据 in 的高低电平区分按下的按键（例如高电平代表按下 1）。在 clk 的上升沿模块接收一个按键信息，同时输出一个 unlock 信号，当 unlock 信号为高电平时表明最近四次输入的序列可以解锁。

首先来考虑如何确定状态。自然，我们可以根据当前最近的四个输入标识状态，则对应的状态共有 24=16 种。但包含十六个状态的有限状态机无论设计上还是实现上都较为复杂，尽管我们可以通过状态化简消去一部分，但这个过程依然是十分繁琐的。

让我们再次分析这个问题。对于一个给定的输入序列，想要判断其能否开锁，我们只需要关注其最近的输入能否组成 0100 序列。先前我们固定观察最近的四次输入，但实际上有些情况近期是一定不能解锁的，例如序列 1110 至少要再经过三次输入才有可能解锁。

基于这一事实，我们可以只关注输入序列是否包含 0100 及其子序列，即考察最近的输入内容为 0、01、010、0010 四种情况。我们称之为后缀识别。

在最开始没有任何输入时，我们可以引入一个初始状态（不妨记作 - ），用于代表不属于上述四种的情况。接下来当输入一个 0 时，我们就识别到了后缀 0，即可进入下一状态；若输入一个 1，则不属于任何一种后缀，因此依然在初始状态。以此类推，我们就得到了下图所示的状态机。

构建流程

于是，我们就可以确定下来，这个问题的状态机一共有五个基本状态。我们约定如下的对应关系：

• S0：对应 -
• S1：对应 0
• S2：对应 01
• S3：对应 010
• S4：对应 0100

初始状态为 S0，仅在 S4 状态时输出解锁信号。由于输出仅和当前状态有关，因此我们可以选择 Moore 型状态机进行设计。五个状态可以使用 3bits 位宽的编码进行处理。

首先定义状态变量以及状态名称：

1
2
3
4
5
6

reg [2:0] current_state, next_state;
localparam S0 = 3'd0;
localparam S1 = 3'd1;
localparam S2 = 3'd2;
localparam S3 = 3'd3;
localparam S4 = 3'd4;

接下来编写第一段：状态更新。假定 reset 信号的效果是清除之前所有的输入，恢复初始状态。则按下 reset 后状态机应当跳转到 S0。

1
2
3
4
5
6

always @(posedge clk) begin
    if (reset)
        current_state <= S0;
    else
        current_state <= next_state;
end

接下来编写第二段：状态转移。根据状态转换图，我们可以编写如下的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

always @(*) begin
    next_state = current_state;
    case (current_state)
        S0: begin   // -
            if (in)
                next_state = S0;    // -
            else
                next_state = S1;    // 0
        end

        S1: begin   // 0
            if (in)
                next_state = S2;    // 01
            else
                next_state = S1;    // 0
        end

        S2: begin   // 01
            if (in)
                next_state = S0;    // -
            else
                next_state = S3;    // 010
        end

        S3: begin   // 010
            if (in)
                next_state = S2;    // 01
            else
                next_state = S4;    // 0100
        end

        S4: begin   // 0100
            if (in)
                next_state = S2;    // 01
            else
                next_state = S1;    // 0
        end
    endcase
end

输出：

1

assign unlock = (current_state == S4) ? 1'B1 : 1'B0;

课堂笔记

另外的表述方式：

另一个例子：

选择器

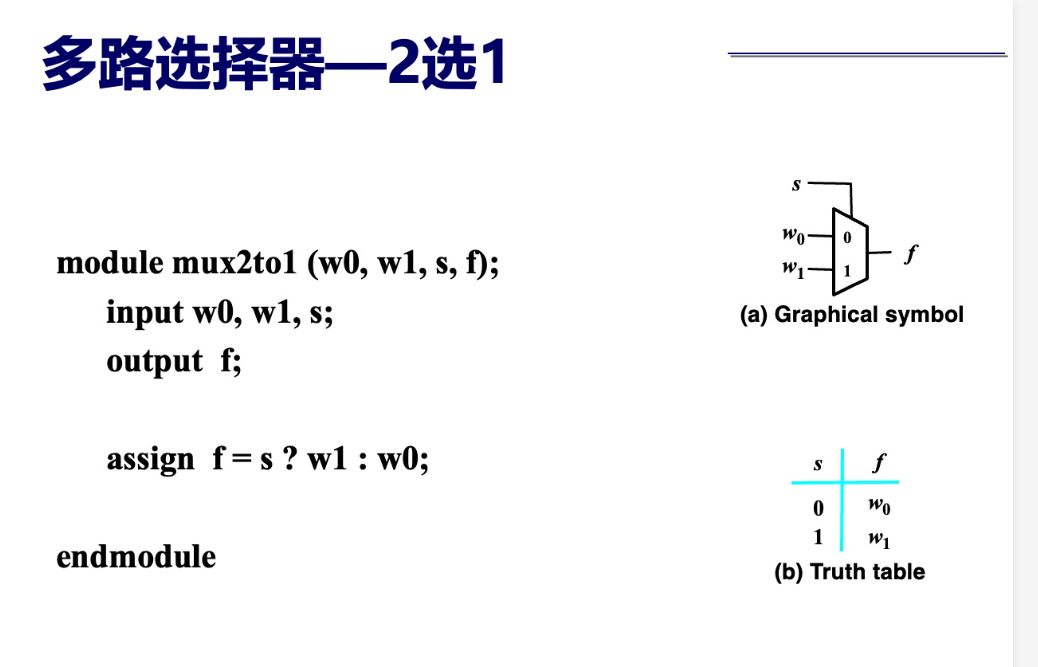
优先级编码器

或者:

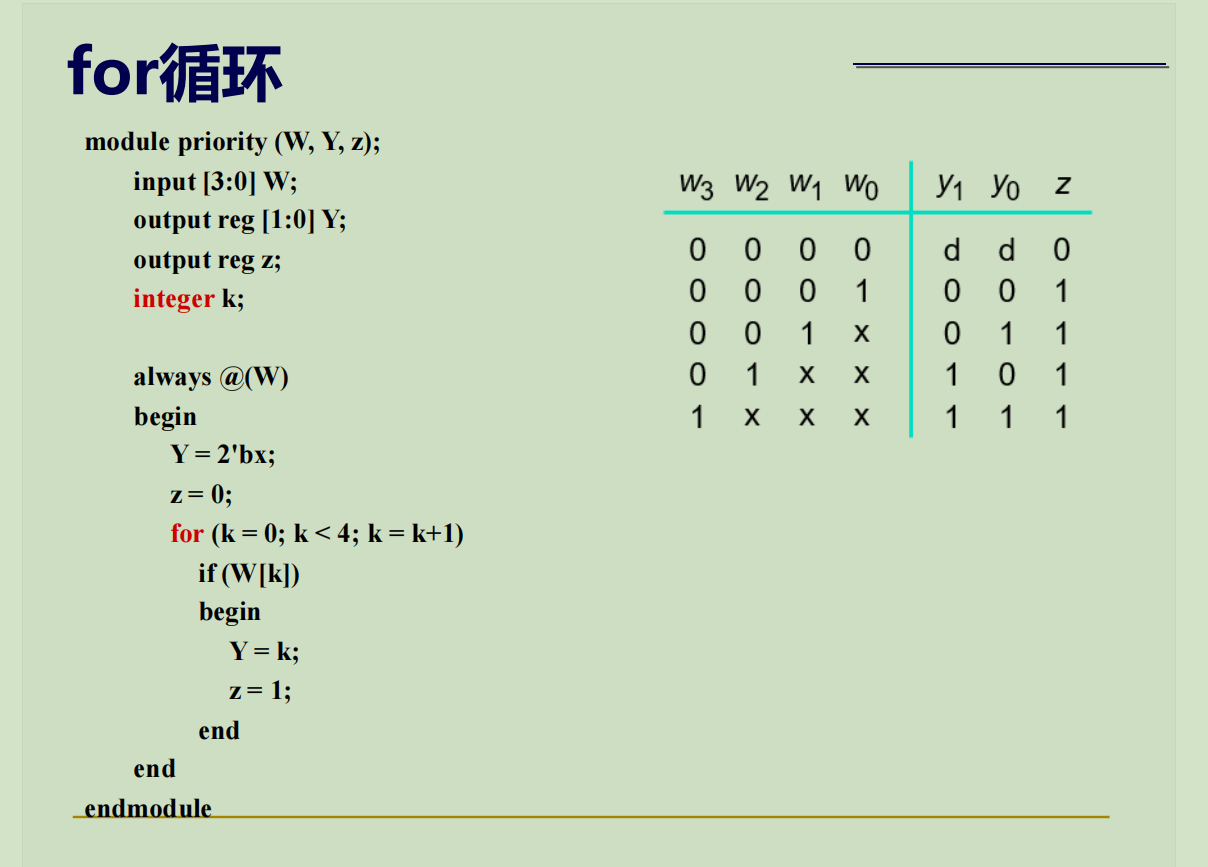
加法器

全加器结构

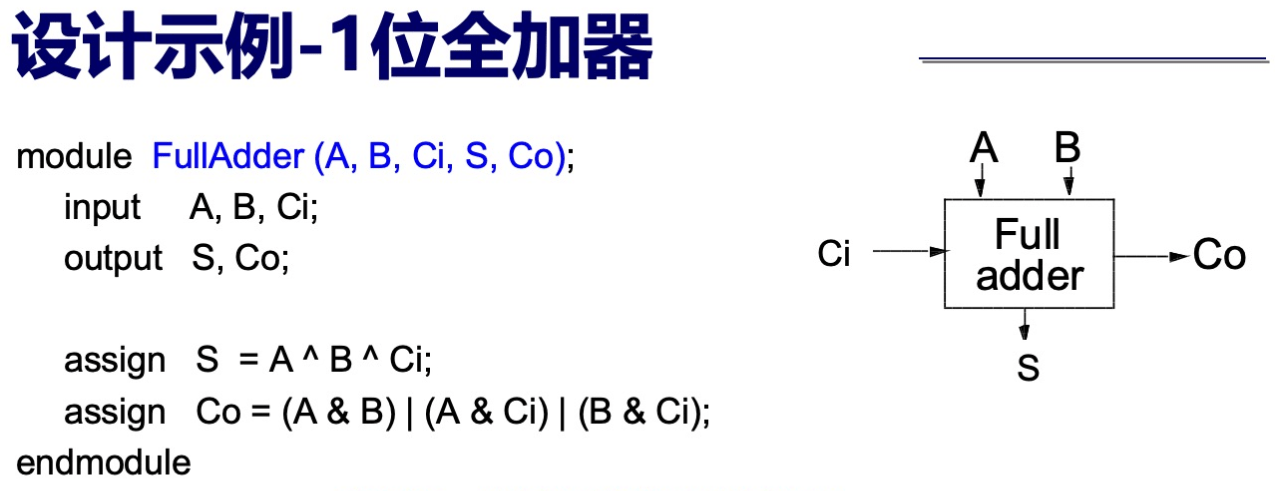
其他内容:组合逻辑电路及其 Verilog 实现

latch 的产生和避免

锁存器,触发器,寄存器

锁存器（Latch），是电平触发的存储单元，数据存储的动作取决于输入时钟（或者使能）信号的电平值。仅当锁存器处于使能状态时，输出才会随着数据输入发生变化。

当电平信号无效时，输出信号随输入信号变化，就像通过了缓冲器；当电平有效时，输出信号被锁存。激励信号的任何变化，都将直接引起锁存器输出状态的改变，很有可能会因为瞬态特性不稳定而产生振荡现象。

锁存器示意图如下：

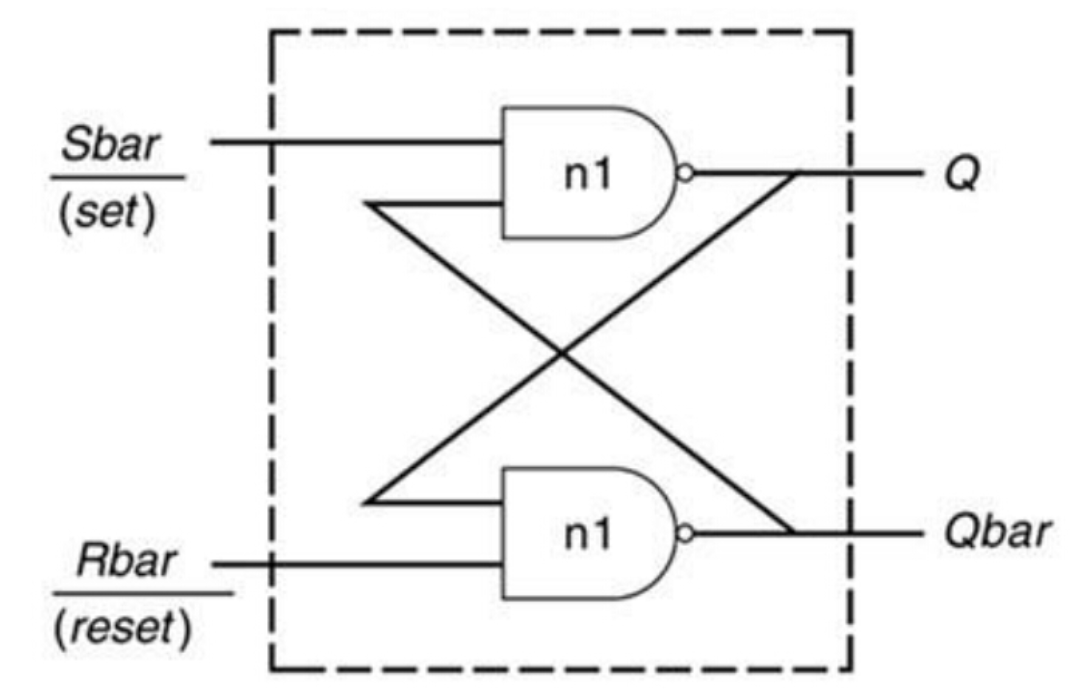
触发器（flip-flop），是边沿敏感的存储单元，数据存储的动作（状态转换）由某一信号的上升沿或者下降沿进行同步的（限制存储单元状态转换在一个很短的时间内）。

触发器示意图如下：

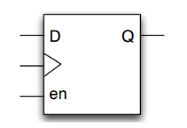
寄存器（register），在 Verilog 中用来暂时存放参与运算的数据和运算结果的变量。一个变量声明为寄存器时，它既可以被综合成触发器，也可能被综合成 Latch，甚至是 wire 型变量。但是大多数情况下我们希望它被综合成触发器，但是有时候由于代码书写问题，它会被综合成不期望的 Latch 结构。

Latch 的主要危害有：

• 1）输入状态可能多次变化，容易产生毛刺，增加了下一级电路的不确定性；
• 2）在大部分 FPGA 的资源中，可能需要比触发器更多的资源去实现 Latch 结构；
• 3）锁存器的出现使得静态时序分析变得更加复杂。

产生原因

1. if 结构不完整

2. case 结构不完整

3. 敏感信号列表不完整

4. 原信号赋值或判断

连续赋值:always 和 initial

过程赋值语句用于对 reg 型变量进行赋值，由 2 种关键字引导，分别是 initial 与 always。这两种语句不可嵌套使用，彼此间 并行 执行（执行的顺序与其在模块中的前后顺序没有关系）。如果 initial 或 always 语句内包含多个语句，则需要搭配关键字 begin 和 end 组成一个块语句。

区别

每个 initial 语句或 always 语句都会产生一个独立的控制流，执行时间都是从 0 时刻开始。二者的区别在于 :

initial 执行一次语句

always 循环执行

格式

敏感变量就是触发 always 块内部语句的条件。加入敏感变量后，always 语句仅在列表中的变量发生变化时才执行内部的过程语句。

1
2
3
4
5
6
7

// 每当 a 或 b 的值发生变化时就执行内部的语句
always @(a or b) begin
    //是的括号里面这东西叫敏感列表
    //所有赋值号右边出现的信号都要放到敏感表里  写全避免latch产生
    //每个数据连接用 or
    [过程语句]
end

有的时候，敏感列表过多，一个一个加入太麻烦，且容易遗漏。为了解决这个问题，Verilog 2001 标准允许使用符号 * 在敏感列表中表示缺省，编译器会根据 always 块内部的内容自动识别敏感变量。

例如，先前的例子可以写为：

1
2
3
4
5

reg Cout;
wire A, B;
always @(*) begin
    Cout = A & B;
end

除了直接使用信号作为敏感变量，Verilog 还支持通过使用 posedge 和 negedge 关键字将电平变化作为敏感变量。其中 posedge 对应上升沿，negedge 对应下降沿。例如：下面的代码仅在 clk 从低电平（0）变为高电平（1）时触发。

1
2
3
4
5
6

reg Cout;
wire A, B, clk;
always @(posedge clk) begin
    Cout <= A & B;
end

assign语句中被赋值的信号定义成wire

过程块中被赋值的信号定义成reg (寄存器 可以改变值的变量形式)

assign 连续赋值

• 与物理线不同但十分相似,Verilog 中的线(和其他信号)是有方向的.这意味着信息只在一个方向上流动,从(通常是一个)源流向汇点(源通常也被称为驱动端,将值驱动到 wire 上).在 verilog 的”连续赋值”(assign)中,右侧的信号值被驱动到左侧的”线”上.请注意:赋值是”连续的”,如果右侧的值发生更改,左侧的值将持续随之改变.(这里与其他语言有很大区别).连续赋值不是一次性事件,其赋值功能是永久持续的.

想要真正理解为啥会这样,你首先要明白,你并不是在编写程序,你其实是在用代码”画”电路! 因此输入端的电平高低的变化必然会影响到 wire 的另一端,你可以想像真的有一根电线连接两个变量.

模块(module)上的端口(port)也有方向(通常是输入 – input 或输出 – output).输入端口由来自模块外部的信号驱动,而输出端口驱动外部的信号.从模块内部查看时,输入端口是驱动源,而输出端口是接收器.

下图说明了电路的每个部分如何对应 Verilog 代码的每个部分.模块和端口声明可以创建黑色盒子的电路.你的任务是通过添加一个 assign 语句来创建一条线(绿色).盒子外的部件不需你考虑,但你应该知道,将测试激励连接到 top_module 上的端口可以来测试黑色盒子电路.

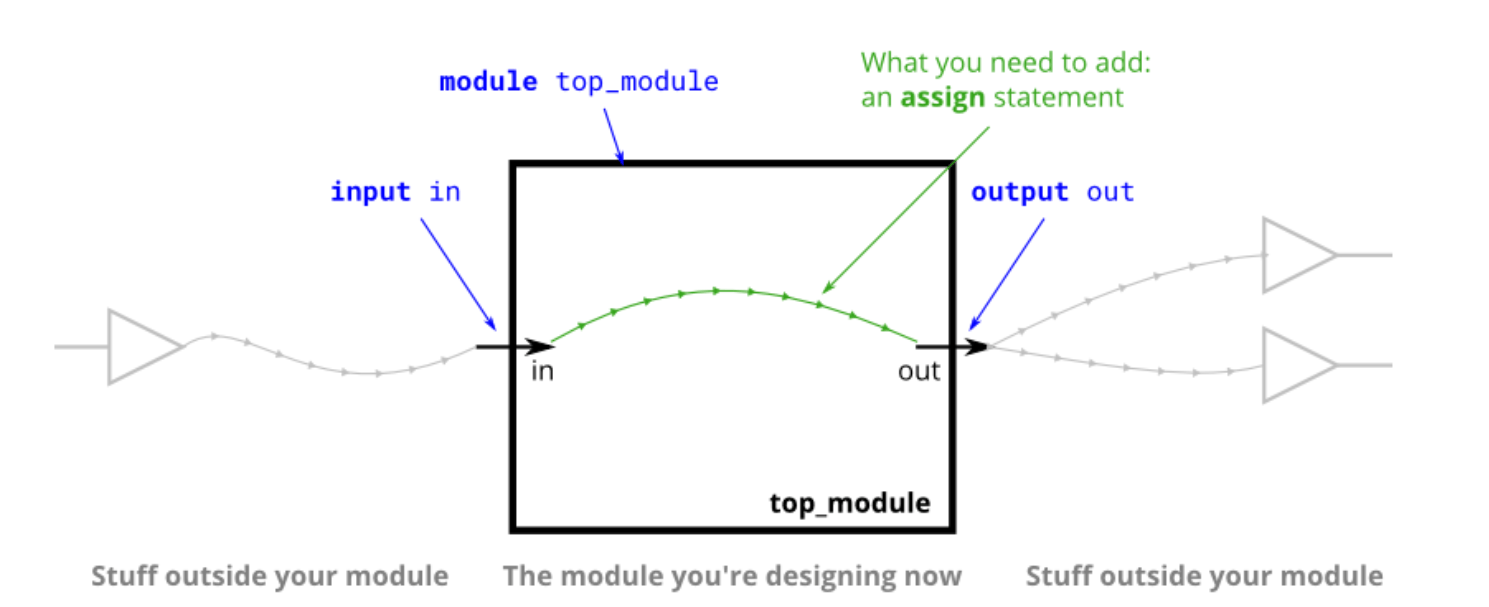
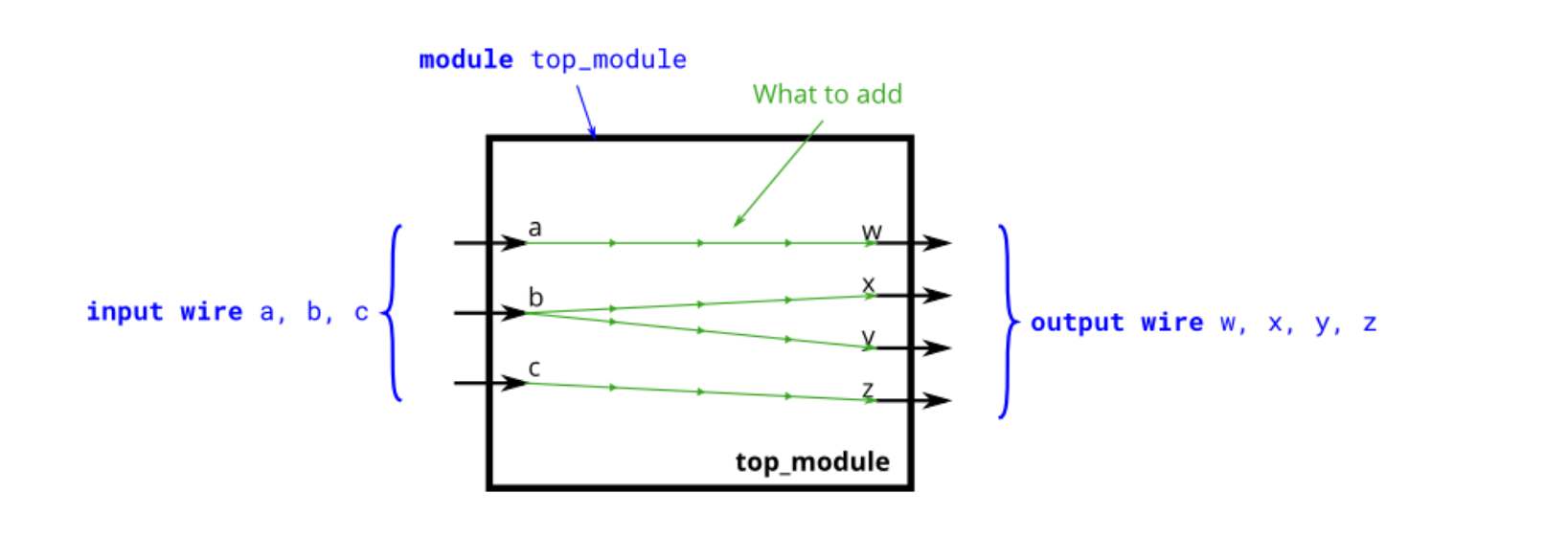
• 下图说明了电路的每个部分如何对应 Verilog 代码的每个部分.模块外部有三个输入端口和四个输出端口.

  当您有多个 assign 语句时,它们在代码中的出现顺序并不重要.与编程语言不同,assign 语句(“连续赋值”)描述事物之间的连接,而不是将值从一个事物复制到另一个事物的操作.

  可能现在应该澄清的一个潜在的困惑来源是:这里的绿色箭头表示电线之间的连接,但不是 wire 本身.模块本身已经声明了 7 条线(名为 A、B、C、W、X、Y 和 Z).这是因为 input 与 output 被声明为了 wire 类型.因此,assign 语句不会创建 wire,而是描述了在已存在的 7 条线之间创建的连接.

  

Verilog 的三种描述层次

• 结构化描述方式：调用其他已经定义过的低层次模块对整个电路的功能进行描述，或者直接调用 Verilog 内部预先定义的基本门级元件描述电路的结构进行描述。
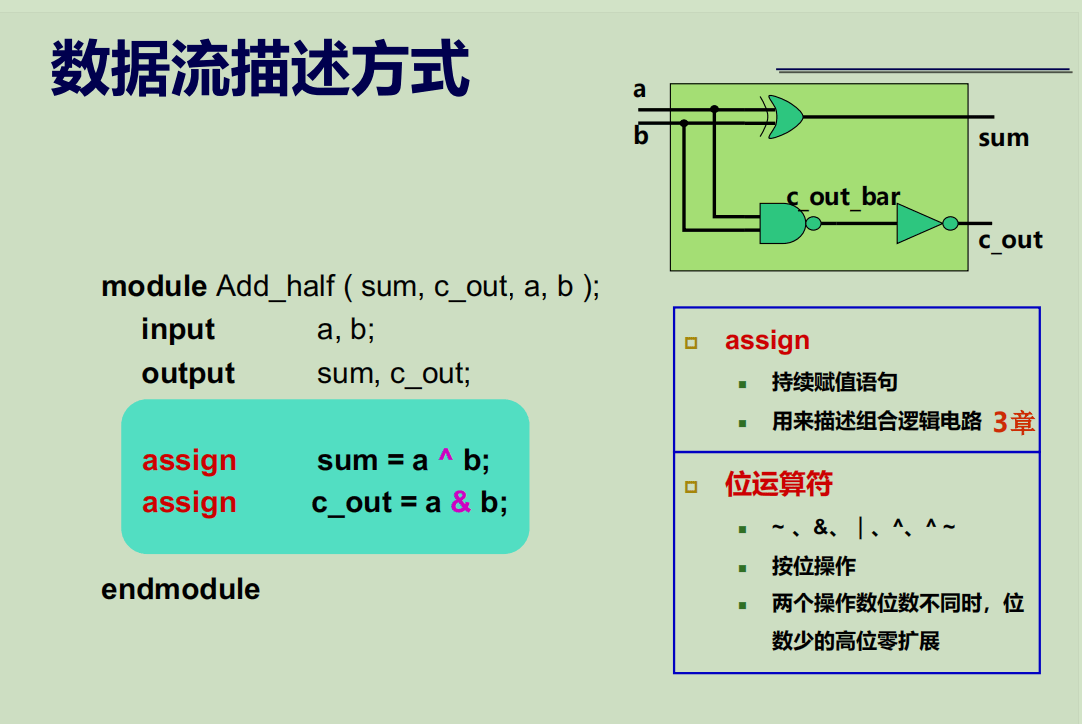
• 数据流描述方式：使用连续赋值语句 assign 对电路的逻辑功能进行描述。该方式特别适合于对组合逻辑电路建模。
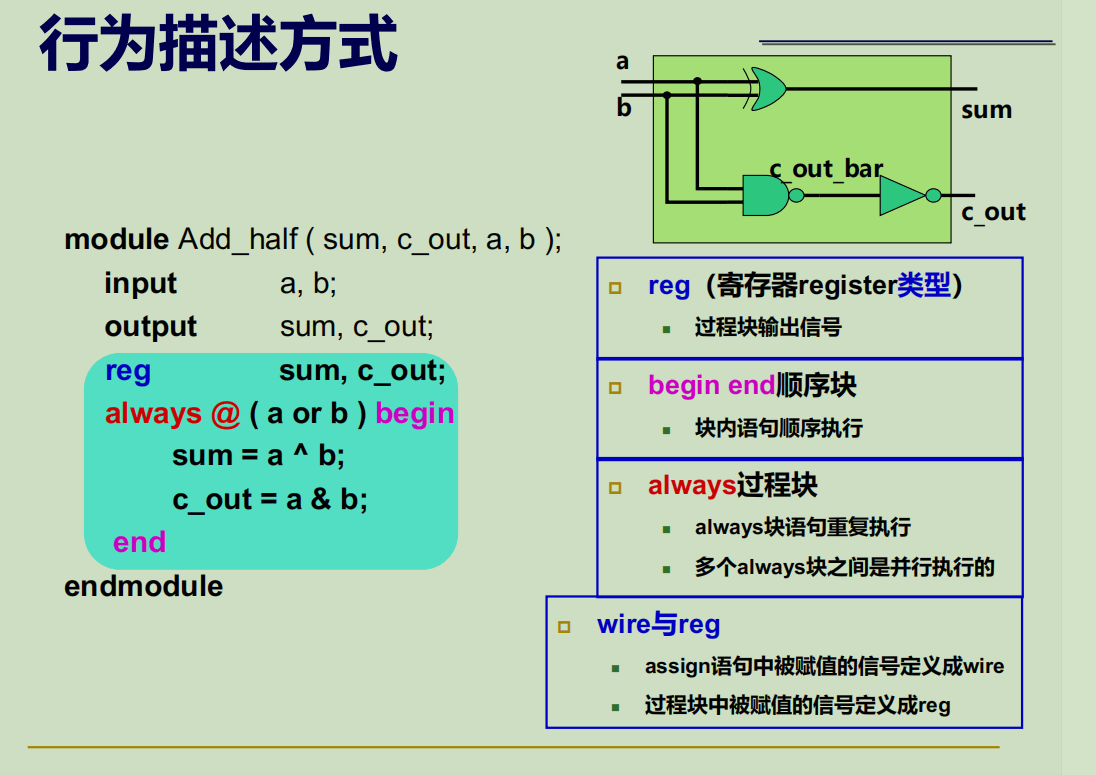
• 行为级描述方式：使用过程块语句结构 always 和比较抽象的高级程序语句对电路的逻辑功能进行描述。

结构化描述方式

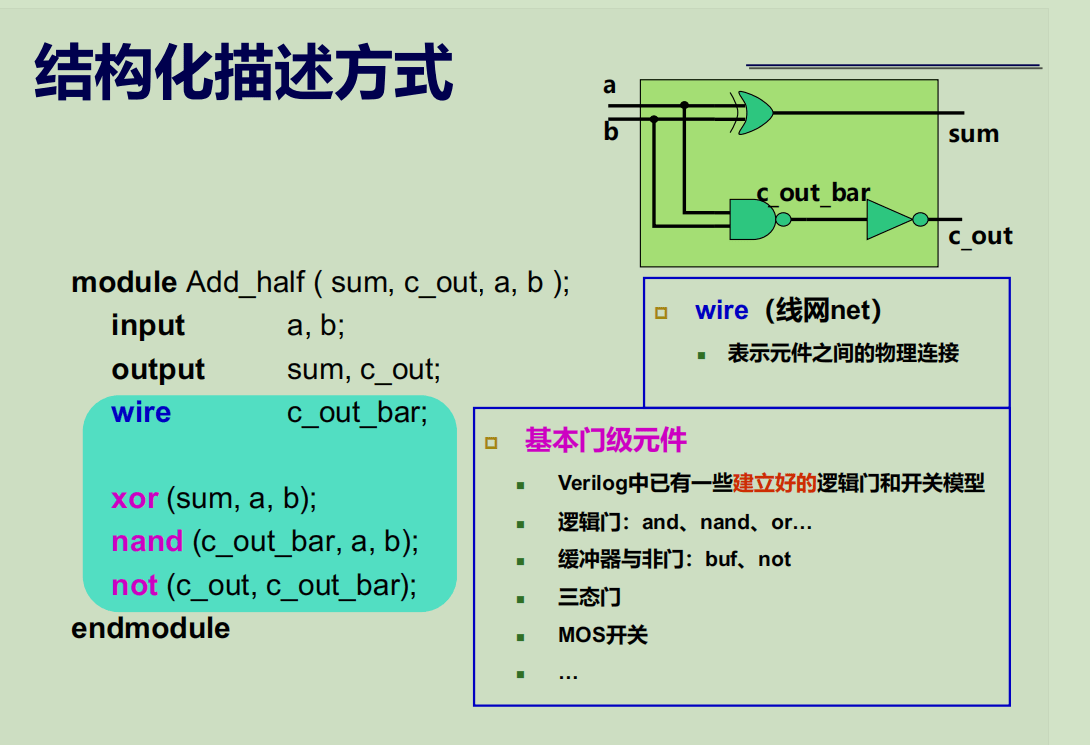
考虑下图所示的电路：

如果从结构化层面来描述电路，我们需要刻画与门、或门和非门，并将其正确连接。

Verilog 常用的内置逻辑门包括：

• and（与门）
• nand（与非门）
• or（或门）
• nor（或非门）
• xor（异或门）
• xnor（同或门）

我们可以通过类似模块例化的方式使用这些逻辑门，进而实现一些简单的逻辑功能。

下面是使用门级单元结构化描述该电路的 Verilog 代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

module MUX2(
    input       a, b,
    input       sel,
    output      out
);

wire and1, and2, sel_not;

and (and1, a, sel_not);
and (and2, b, sel);
not (sel_not, sel);
or (out, and1, and2);

endmodule

数据流描述方式

数据流描述方式需要我们得到逻辑表达式。可以将门电路转换为对应的逻辑表达式：

1
2
3
4

and (and1, a, sel_not);     // and1 = a & sel_not
and (and2, b, sel);         // and2 = b & sel
not (sel_not, sel);         // sel_not = ~sel
or (out, and1, and2);       // out = and1 | and2

化简得到输出 out 关于输入 a、b 和 sel 的逻辑表达式：

1

out = (a & ~sel) | (b & sel);

由此可以得到基于 assign 语句的数据流描述。

1
2
3
4
5
6
7
8
9

module MUX2(
    input       a, b,
    input       sel,
    output      out
);

assign out = (a & ~sel) | (b & sel);
endmodule

行为级描述方式

很多时候，我们难以得到模块的电路结构，或者得到的结构十分繁琐，这时我们就可以使用行为级描述，以类似于高级语言的抽象层次进行硬件结构开发。这一层面的描述过程更看重功能需求与算法实现，也是对于我们最为友好的描述方式。

下面是该电路的行为级描述代码。

1
2
3
4
5
6
7
8
9
10
11
12
13

module MUX2(
    input       a, b,
    input       sel,
    output reg  out
);
always @(*) begin
    if (!sel)
        out = a;
    else
        out = b;
end
endmodule

数据表示方式